
| Suchen | Themen | Lexikon |
| Register | Fächer | Datenbank |
| Medien | Links | Daten | |
| Projekte | Dokumente | ||
| Schule und Agenda 21 | |
| Lokale Agenda | Globale Agenda |

 |
|
|
|
 |
||||||||||||||||||
| Kontakt | Haftungsausschluss |
|
|||
|
|
|||||
| Hintergrund | |||||||||||||||||||||||||
Diese Seite behandelt die Einkommensteuer in Deutschland. |
|||||||||||||||||||||||||
 Daten/Großansicht |
Bedeutung der Einkommensteuer für den Staatshaushalt |
||||||||||||||||||||||||
Verteilung der Einkommensteuer |
|||||||||||||||||||||||||
|
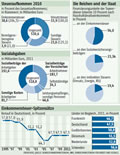
Einkommensteuer DE 2019  17.05.24 (2461) |
dpa-Globus 16850: Wer zahlt wie viel Steuern? Die Grafik stellt die Einkommensteuerverteilung für das Jahr 2024* mittels Dezilen dar, wobei die beiden unteren zum untersten Fünftel zusammengefasst sind Das untere Fünftel mit einem zu versteuerndem Einkommen (zvE) unter 15.175 € zahlt nur 0,3 % der gesamten Einkommensteuer, denn laut BVG darf das Existenzminimum nicht besteuert werden. Daher wird nur das den Grundfreibetrag übersteigende Einkommen besteuert. Mit wachsendem zvE wächst der Anteil am Steueraufkommen bis auf 56,9 % beim obersten Dezil, denn in Deutschland ist der Steuertarif progressiv, allerdings nur bis zum Spitzensteuersatz von 45 %. Jedoch sind Reiche, deren Einkommen zum großen Teil aus Zinsen/ Dividenden besteht, von der Progression weitestgehend ausgenommen, denn Einkünfte aus Kapitalvermögen werden seit der Steuerreform 2009 nur noch pauschal mit der Abgeltungsteuer von 25 % besteuert.
Quelle: Bundesfinanzministerium | Infografik | Tabelle/Infos | Serie
|
||||||||||||||||||||||||
| Einkommensteuergesetz: Grundzüge | |||||||||||||||||||||||||
Das Einkommensteuergesetz (EStG) Deutschlands ist sehr kompliziert und es werden daher im Folgenden nur die Grundzüge dargestellt.
|
|||||||||||||||||||||||||
Die Einkünfte aus Kapitalvermögen werden gesondert behandelt mittels der Abgeltungsteuer. (§ 32d EStG). Bei den anderen sechs Einkunftsarten werden die Einkünfte im Prinzip jeweils als Saldo Einnahmen minus Ausgaben bestimmt, wobei allerdings eine Fülle von Regelungen im Detail das Berechnungsverfahren komplizieren. |
|||||||||||||||||||||||||
Das "zu versteuernde Einkommen" (zvE) ist dann die |
|||||||||||||||||||||||||
| Existenzminimum-bericht |
Das Existenzminium wird tournusmäßig alle 2 Jahre durch die Bundesregierung im Existenzminimumbericht festgelegt und der Grundfreibetrag entsprechend erhöht. |
||||||||||||||||||||||||
| Einkommensteuer-Tarife | |||||||||||||||||||||||||||
| Der in §32a Einkommensteuergesetz (EStG) definierte Steuertarif wird "Grundtarif" genannt. Er regelt direkt die Besteuerung von Einzelpersonen und definiert über eine einfache Transformation auch den "Splittingtarif", der früher nur für zusammenveranlagte Ehepaare galt, nach BVG-Urteil vom 7.5.13 aber auch rückwirkend zum 1.8.2001 für eingetragene Lebenspartnerschaften
[70] [71] [72] . Auch das aktuell diskutierte "Familiensplitting" wird durch den Grundtarif definiert, denn es ist der bisherige Splittingtarif mit einem variablen Splittingfaktor, bei dem neben den Eltern auch die Kinder berücksichtigt werden (bisher Faktor konstant = 2). Der Grundtarif ist also die Basis aller Steuertarife und Steuersätze. Der Grundtarif hat im Prinzip folgenden dreigeteilten Verlauf:
|
|||||||||||||||||||||||||||
| |
(1) Grenzsteuersatz: Änderungsrate des Steuertarifs = Steuersatz, mit dem eine kleine Einkommensänderung zu versteuern ist [81] (Anstieg der Steuerfunktion [82] ). (2) Eingangssteuersatz = Grenzsteuersatz am Anfang der Progressionszone, also für das zu versteuernde Einkommen, das um 1 € größer ist als der Grundfreibetrag, ab 2009: 14 % (Online-Rechner mit x = g0 + 1) (3) Spitzensteuersatz = Grenzsteuersatz in der Proportionalzone ab 2007: 42 % | 45 % (Reichensteuer) (s. Parametertabelle) Der Grenz-, Differenz und Effektivsteuersatz können mit dem Online-Rechner ermittelt werden. Bei den Tarifen der vergangen Jahre wurde Zone b) noch einmal unterteilt und ab dem Jahr 2007 auch die Zone c) durch Einführung der sog. "Reichensteuer". |
||||||||||||||||||||||||||
| Tarifverlauf Grenzsteuersatz |
Meist wird nicht die eigentliche Steuerfunktion dargestellt sondern der Grenzsteuersatz, also die Änderungsrate der Steuerfunktion (Mathematik: Ableitung), die ab 2007 in fünf Zonen aufgeteilt ist. Daten für die Jahrgänge ab 2004: Parametertabelle | ||||||||||||||||||||||||||
|
Einkommensteuer Grundtarif DE 2026  23.01.26 (2725) |
dpa-Globus 18092: Der Einkommensteuer-Tarif 2026 Damit das Existenzminimum steuerfrei bleibt, wird im Einkommensteuergesetz ($32a EStG) der Grundfreibetrag festgelegt, bis zu dem die Steuer null ist. Um die "Kalte Progression" zu mildern, wurden auch zwei Folge-Eckwerte im Steuertarif etwas erhöht. Die Grafik zeigt den Grenzsteuersatz-Verlauf im Grundtarif. Er wird abschnittsweise für fünf Zonen definiert:
Hinzu kommt der Solidaritätszuschlag (kurz: „Soli“, Abk. „SolZ“) auf einen Steuerbetrag über der Freigrenze 20.350 € bei zvE 74.968 € . Darüber ("Milderungszone" ↗pdf) steigt der Soli linear von 0% auf 5,5%, so dass ab zvE 116.606 € konstant 5,5% auf den vollen Steuerbetrag entfallen (Splitttarif: alle Grenzen 2-fach). Die Einkommensteuer (inkl. Lohnsteuer) und die Mehrwertsteuer sind die beiden mit Abstand ergiebigsten Steuerquellen des Staates: 34,2% + 31,9% = 66,1% der gesamten Steuereinnahmen im Jahr 2024 (➔). Quelle: BMF bpb | Infografik | Serie
|
||||||||||||||||||||||||||
| Grundtarif: Berechnungsverfahren und Parameter | |||||||||||||||||||||||||||
Da der Tarif fast jedes Jahr geändert wird (z.B. durch Erhöhung des Grundfreibetrags), ist es zweckmäßig, ihn in parametrisierter Form darzustellen, d.h. mit Kurzbezeichnungen für die konkreten Zahlenwerte. Ab dem Jahr 2004 wird die Einkommensteuer nach folgendem Rechenschema berechnet. Dabei bezeichnet x das auf volle Euro abgerundete "zu versteuernde Einkommen (zvE)" (s.o), der zu berechnende Steuerbetrag ist eine Funktion von x und wird mit Grundtarif (x) bezeichnet. |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
Grundtarif: Parameter-Tabelle |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quelle für Tarif 2025: BMF |
| Splittingtarif | |
| Zur Förderung von Ehepaaren wurde für sie der "Splittingtarif" eingeführt, bei dem der Durchschnitt ihrer Einkünfte mittels Grundtarif versteuert und dieser Steuerbetrag anschließend verdoppelt wird: Splittingtarif ( x1 + x2 ) = 2 • Grundtarif ( (x1 + x2) / 2) ) Falls beide Einkommen in der selben Proportionalzone liegen, stimmen Splittingtarif und Einzelversteuerung überein, d.h. Splittingtarif ( x1 + x2 ) = Grundtarif ( x1 ) + Grundtarif ( x2 ) [85] , andernfalls ist der Splittingtarif deutlich günstiger, da der Anstieg der Steuerfunktion zunimmt (Progressionszone) oder gleich bleibt (Proportionalzone) [86] . Falls ein Einkommen 0 ist (typischerweise: Hausfrauen-Ehe [53]), folgt für das dann einzige Einkommen x: Splittingtarif ( x ) = 2 • Grundtarif ( x / 2 ) Der Splittingtarif ist bis zum doppelten Grundfreibetrag 0 und steigt danach zunächst deutlich langsamer an als der Grundtarif [87]. Er liegt bis weit in die Progressionszone sogar unter der Hälfte des Grundtarifs: beim Tarif 2010-12 bis rund 29.900 €; beim Tarif 2013 bis rund 30.300 €; beim Tarif 2014 bis rund 31.000 € (s.Online-Rechner ). Bis zur doppelten Grenze der Progressionszone wächst der absolute Unterschied der beiden Tarife und bleibt danach zunächst konstant = n1 (2012: 8172 €; 2013: 8196 €). Bei sehr hohen Einkommen vergrößert die Reichensteuer den Abstand auf maximal n2 (2012: 15.694 €; 2013: 15.718 €). Der Grenzsteuersatz ist dann der Spitzensteuersatz, dem sich der Effektivsteuersatz immer mehr annähert [88] . |
|
 Daten/Großansicht |
Der im vorigen Abschnitt beschriebene Einspareffekt des Splittingtarifs im Vergleich zur Einzelversteuerung nach Grundtarif belastet den Staatshaushalt erheblich: Im Jahr 2010 mit rund 20 Mrd. €. Hinzu kommen weitere sich auf Ehepaare (auch ohne Kinder) beziehende staatliche Leistungen im Umfang von 55 Mrd. €, zusammen also 75 Mrd.€
[54]. Über die Jahre summieren sich die staatlichen Aufwendungen z.B. pro Hausfrauenehe auf über eine halbe Million Euro
[55]. Der Splittingtarif wurde ursprünglich eingeführt, um die Betreuung und Erziehung von Kindern im Rahmen der Familie (i.d.R. in Form der traditionellen Hausfrauenehe) steuerlich zu subventionieren. Er ist über die Jahre immer mehr in die Kritik geraten [56] . Es wird daher zunehmend gefordert, das Splitting nur auf Familien mit Kindern anzuwenden oder ganz abzuschaffen und stattdessen die Kinderbetreuung und - erziehung auf geeignetere Weise staatlich zu fördern. |
| Familiensplitting | |
| Als eine Reform des bisherigen in die Kritik geratenen Ehegatten-Splittings wird das sog. "Familiensplitting" vorgeschlagen: Der Splittingtarif soll nur dann zur Anwendung kommen, falls steuerrechtlich zu berücksichtigende Kinder oder Jugendliche (in Schule oder Ausbildung bis zu einem Alter von z.B. 25 Jahre) Teil der Familie sind. Ergänzend könnte der Splittingtarif modifiziert werden, indem der bisherige konstante Splittingfaktor 2 ersetzt wird durch einen variablen Familienfaktor F, also: Splittingtarif ( x ) = F • Grundtarif ( x / F) Es sind verschiedene Varianten zur Berechnung des Familienfaktors F denkbar, z.B. könnten Erwachsene und Kinder mit unterschiedlichen Zählwerten eingehen, z.B. Eltern jeweils mit dem Wert 1 und Kinder jeweils mit dem Wert 0,5. Für eine Familie mit 2 Eltern und 2 Kindern ergibt sich der Faktor F = 1 +1 + 0,5 + 0,5 = 3. Im folgenden Online-Rechner wird diese Modellvariante mit 3 als Vorgabewert gerechnet [57] . Bei dieser Variante des Familiensplittings fallen deutlich weniger Steuern als beim bisherigen Splitting an: Bis zum 3-fachen Grundfreibetrag (2014: 3 • 8354 = 25.062) ist der Steuerbetrag = 0, danach steigt er deutlich langsamer an; er beträgt z.B. beim Tarif 2014 bis knapp unter 70.000 € weniger als die Hälfte des Grundtarifs. Der absolute Unterschied zwischen Grundtarif und Familiensplitting wächst bis auf ein Maximum von 2 • n (2014: 2 • 15.761 = 31.522). |
|
| Kalte Progression | |
| Mit "kalter" Progression wird der Effekt bezeichnet, wenn trotz Lohnerhöhung die Kaufkraft sinkt. Ursache dafür ist a) die Progression im Steuertarif und b) die Inflation. Zunächst ist zu beachten, dass a) alleine nicht die kalte Progression bewirken kann, weil dazu der Differenzsteuersatz mindestens 100 % sein müsste, was aber bei weitem nicht der Fall ist. Er ist nur etwas größer als der Grenzsteuersatz, dessen Maximum der Spitzensteuersatz von aktuell 45 % ist, also weniger als die Hälfte von 100 % [91]. Damit insgesamt die Kaufkraft sinkt, muss die Inflationsrate hinreichend groß sein, mindestens etwas mehr als die Hälfte der Lohnerhöhung [92] . Bei der zuletzt (Ende 2021) wieder stark gestiegenen Inflation (rund 5%) wird diese Schwelle überschritten. Die inzwischen jährliche Anpassung des Steuertarifs (Erhöhung des Grundfreibetrags und der Eckwerte) soll die Kalte Progression abmildern. |
|
| Berechnungen mit Online-Rechner | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Um die Entwicklung der Steuerbeträge und Steuersätze im Zeitverlauf einfach vergleichen zu können, listet die folgende Tabelle alle Steuerbeträge und - sätze der letzten 10 Jahre. Die Steuer wird nach gleichem Algorithmus berechnet, nur die Parameter ändern sich jedes Jahr. Nach Eingabe des zu versteuernden Einkommens (zvE) (ggf. auch Splittfaktor; Differenz) werden jeweils 3 Werte als Trippel, durch | getrennt, gelistet. Steuerbetrag bzw. Steuersatz gemäß: Grundtarif | Splittingtarif | Familiensplitting Das Familiensplitting ist bisher nicht Teil des Steuergesetzes sondern ein in Parteien und Medien diskutierter Vorschlag zur Reform des bisherigen Ehegattensplittings. In der hier berechneten Variante wird der konstante Faktor 2 des bisherigen Splittingtarifs durch einen variablen Faktor F ersetzt, der neben dem zu versteuernden Einkommen x und der Einkommensdifferenz Δx interaktiv eingegeben werden kann. Aus der Definition des Splittingtarifs folgt, dass sich der bisherige Splitting- bzw. Grundtarif als Spezialfall des neuen Familiensplittings ergeben, nämlich bei Eingabe von F=2 bzw. F=1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x: auf volle Euro abgerundetes* "zu versteuerndes Einkommen" (zvE) (s.o.) (Vorgabe: 50.000 €, max. 10 Mio. € ) F: Faktor für das Familiensplitting* (Vorgabe: F = 3; min = 1; max = 10) Δx: Einkommensdifferenz zur Berechunung des Differenzsteuersatzes (Vorgabe: 1.000 €; max = 1 Mio) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Effektivsteuersatz = Durchschnittssteuersatz = E(x) / x Grenzsteuersatz = Änderungsrate des Steuertarifs = Anstieg der Steuerfunktion = E´ (x) [89] Differenzsteuersatz = Steuerdifferenz / Einkommensdifferenz = ΔE / Δx; ΔE = E(x+Δx) - E(x) [90] |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
* Hinweis zum Splittingfaktor: Bisher ist der Faktor konstant 2, bei Einführung des Familiensplittings könnte er variabel werden, z.B. pro Elternteil 1, pro Kind 0,5, also bei 2 Eltern + 2 Kindern: Faktor = 3. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Berechnungen mit Tabellenkalkulation | |||||||||||||||||||||
|
Der obige Online-Rechner eignet sich für die Berechnung einzelner Werte, wer aber z.B. Wertetabellen anlegen will oder die Steuerfunktion für eigene Berechnungen, z.B. die Erstellung der Einkommensteuererklärung, verwenden will, wird ggf. motiviert sein, den Steuertarif selbst im Rahmen einer Tabellenfunktion zu programmieren, um aufwändige Rechnungen durch Automatisieren effektiv erledigen zu können. Die folgenden Hinweise sollen dazu eine Hilfestellung bieten. Sie gelten für den Steuertarif ab 2004. |
|||||||||||||||||||||
| Programmierung der Steuerfunktion | |||||||||||||||||||||
|
Der Grundtarif (s. Berechnungsverfahren) wird programmiert als Fallunterscheidung,
wobei x das abgerundete "zu versteuernde Einkommen" (zvE) ist. Das Mal-Zeichen • wird durch * ersetzt, die Indizierung der Parameter wird ohne Tiefstellung dargestellt, da sie in Tabellenkalkulationen und Programmiersprachen nicht üblich ist. Zur Vereinfachung unterbleibt die Berechung der in § 32a EStG definierten Zwischenwerte y, z, in dem sie durch ihren Funktionsterm ersetzt werden: |
|||||||||||||||||||||
| Variante 1 |
Falls x ≤ g0 dann steuer = 0 sonst falls x ≤ g1 dann steuer = (a1 * (x - g0) /10000 + b1) * (x - g0) /10000 sonst falls x ≤ g2 dann steuer = (a2 * (x - g1) /10000 + b2) * (x - g1) /10000 + c2 sonst falls x ≤ g3 dann steuer = m1 * x - n1 sonst steuer = m2 * x - n2 |
||||||||||||||||||||
| Der Vergleichsoperator "≤" wird üblicherweise in Programmiersprachen als "<=" geschrieben. Falls das Probleme bereitet kann das Berechnungsverfahren auch in umgekehrter Reihenfolge mit dem Operator ">" dargestellt werden. Diese Variante eignet sich besonders für die weiter unten beschriebene Programmierung der Fallunterscheidung mittels Schachtelung der Wenn( )-Anweisung. |
|||||||||||||||||||||
| Variante 2 für Wenn- Schachtelung (s.u.) |
Falls x > g3 dann steuer = m2 * x - n2 sonst falls x > g2 dann steuer = m1 * x - n1 sonst falls x > g1 dann steuer = (a2 * (x - g1)/10000 + b2) * (x - g1)/10000 + c2 sonst falls x > g0 dann steuer = (a1 * (x - g0)/10000 + b1) * (x - g0)/10000 sonst steuer = 0 |
||||||||||||||||||||
Falls die verwendete Tabellenkalkulation eine Programmierung ermöglicht, bietet es sich an, die Fallunterscheidung als Funktion zu programmieren und dabei alle Parameter zu übergeben, z.B. in der Programmiersprache Visual-Basic für Excel-Tabellen. |
|||||||||||||||||||||
| Grundtarif (...) | Grundlage für alle weiteren Funktionen ist die Funktion "Grundtarif" mit einer Parameterliste für jeden Jahrgang. Mit dieser Funktion werden alle weiteren programmiert. |
||||||||||||||||||||
| Verwendung von Punkt und Komma |
Achtung: Programmiersprachen verwenden i.d.R. die im Englischen gültigen Schreibweisen für Dezimalzahlen, also den Punkt (statt Komma im Deutschen)
als Trennzeichen vor dem Bruchteil. Das Komma dient dagegen i.d.R. als Trennzeichen in der Parameterliste. Diese Variante wird im Folgenden verwendet. Bei jedem Jahrgang müssen jeweils 13 Parameter aus der obigen Parametertabelle übergeben werden. |
||||||||||||||||||||
| Grundtarif 2021 |
Function Grundtarif21(x) |
||||||||||||||||||||
| Splittingtarif 2021 |
Function Splittingtarif21(x) Splittingtarif21 = 2 * Grundtarif21(x / 2) end function |
||||||||||||||||||||
|
|||||||||||||||||||||
Falls keine Programmiersprache verwendet werden kann, bieten die meisten Tabellenkalkulationen die Fallunterscheidung mit der Funktion Wenn( ) an: |
|||||||||||||||||||||
Laut § 32a EStG ist der Steuerbetrag auf den nächsten ganzen Euro abzurunden. Die meisten Tabellenkalkulationen bieten dafür geeignete Funktionen, deren Bezeichnung jedoch nicht einheitlich ist. Heißt die Funktion z.B. "Abrunden", so ergibt sich folgende Eingabezeile für die entsprechende Zelle der Tabellenkalkulation: |
|||||||||||||||||||||
| Eingabezeile Kopiervorlage |
= Abrunden ( Wenn( .... ); 0) |
||||||||||||||||||||
| Variante mit Parametern in benannten Zellen |
Zur möglichst lesbaren und direkten Umsetzung dieses Konzepts werden die Parameter in entsprechend benannte Extrazellen geschrieben. In der obigen Wenn( )-Schachtelung ist dann x durch Spalte A zu ersetzen
|
||||||||||||||||||||
| Variante ohne Parameter als Symbole |
Falls auf benannte Extrazellen für die Parameter verzichtet werden soll, sind in der Parameterliste statt der Symbole g0, g1 usw. die konkreten Zahlenwerte der Parameter aus der Parametertabelle einzusetzen, wodurch sehr lange unübersichtliche Zeichenketten entstehen. Zur Fehlervermeidung empfiehlt sich, diese Zeile mittels der Funktion "Suchen und Ersetzen" in einer Textverarbeitung zu erstellen. Für die Jahrgänge ab 2014 können die entsprechenden Zeilen der Kopiervorlage (txt, unformatiert) entnommen werden. |
||||||||||||||||||||
| Berechnungen mit Taschenrechner | |
| Da die Teilfunktionen des Grundtarifs nach dem für Berechnungen günstigen Horner-Schema angegeben sind, können die Rechnungen auch mit dem Taschenrechner leicht durchgeführt werden, zumal nur die Basisoperatoren benötigt werden. Vorausgesetzt wird aber, dass der Taschenrechner einen Speicher für ein Zwischenergebnis hat. Verwendet werden die Parameter vom Grundtarif 2010-2012: Auf die Berechnung der Zwischenergebnisse y, z wird verzichtet, da sie elementar ist. Achtung: Beim Taschenrechner wird in den Zahlen der Punkt (nicht das Komma) als Trennzeichen vor dem Bruchteil verwendet. |
|
| Nullzone | Das zu versteuernde Einkommen (zvE) betrage 8000 €: da 8000 < Grundfreibetrag (8004): Einkommensteuer = 0, |
| Progressionszone I | Das zvE betrage 12000 €, also ist y = 0,3996 [abspeichern], dann die Tippfolge: x 912.17 + 1400 = [Anzeige: 1764.50...] x Speicher = [Anzeige: 705.095....]. Dieser Wert wird abgerundet auf 705. |
| Progressionszone II | Das zvE betrage 30000 €, also ist z = 1.6531 [abspeichern], dann die Tippfolge: x 228.74 + 2397 = [Anzeige: 2775.13..] x Speicher + 1038 = [Anzeige: 5625.567....] Dieser Wert wird abgerundet auf 5625. |
| Proportionalzone I | Das zvE betrage 70000 €: : Tippfolge: 0.42 x 70000 - 8172 = [Anzeige: 21228] Dieser Wert ist schon ganzzahlig, also 21228. |
| Proportionalzone II | Das zvE betrage 260000 €: Tippfolge: 0.45 x 260000 - 15694 = [Anzeige: 101306] Dieser Wert ist schon ganzzahlig, also 101306. |
|
|
|
|
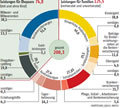
Einkommensteuer Grundtarif DE 2026  23.01.26 (2725) |
dpa-Globus 18092: Der Einkommensteuer-Tarif 2026 Damit das Existenzminimum steuerfrei bleibt, wird im Einkommensteuergesetz ($32a EStG) der Grundfreibetrag festgelegt, bis zu dem die Steuer null ist. Um die "Kalte Progression" zu mildern, wurden auch zwei Folge-Eckwerte im Steuertarif etwas erhöht. Die Grafik zeigt den Grenzsteuersatz-Verlauf im Grundtarif. Er wird abschnittsweise für fünf Zonen definiert:
Hinzu kommt der Solidaritätszuschlag (kurz: „Soli“, Abk. „SolZ“) auf einen Steuerbetrag über der Freigrenze 20.350 € bei zvE 74.968 € . Darüber ("Milderungszone" ↗pdf) steigt der Soli linear von 0% auf 5,5%, so dass ab zvE 116.606 € konstant 5,5% auf den vollen Steuerbetrag entfallen (Splitttarif: alle Grenzen 2-fach). Die Einkommensteuer (inkl. Lohnsteuer) und die Mehrwertsteuer sind die beiden mit Abstand ergiebigsten Steuerquellen des Staates: 34,2% + 31,9% = 66,1% der gesamten Steuereinnahmen im Jahr 2024 (➔). Quelle: BMF bpb | Infografik | Serie
|
||||||||||||||||||||||||||
|
Steuereinnahmen DE 1997-2024  30.05.25 (2621) |
dpa-Globus 17605: Steuereinnahmen Im Jahr 2024 stiegen die gesamten Steuereinnahmen in Deutschland um 3,5% auf einen neuen Rekordstand von 947,7 G€ ƵR , davon wurden 75,9% über die gemeinschaftlichen Steuern (u.a. Lohn-/Einkommensteuer, Umsatzsteuer) und 10,9% über die Bundessteuern (u.a. Energiesteuer, Solidaritätszuschlag) erhoben. (→ Steuerspirale).
Quelle: BMF: 1.Finanzbericht 2025 2.Zeitreihe 3.Steuerschätzung | Infografik | Serie | Zeitreihe
|
||||||||||||||||||||||||||
|
Steuerspirale DE-2024  16.05.25 (2617) |
dpa-Globus 17576: Steuerspirale 2024 Im Jahr 2024 hat der Staat (Bund, Länder, Gemeinden) 947,7 G€ Steuern eingenommen (+3,5 % ggü.Vorjahr).
Quelle: BMF | Infografik | Tabelle/Infos | Serie
|
||||||||||||||||||||||||||
|
|
|
| Jahrgang: | 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
|
|
|
Aktionsplan Ungleichheit 19.01.15 (118) |
Oxfam: Besser gleich! Schließt die Lücke zwischen Arm und Reich! Laut Oxfam hat die Ungleichheit bei Einkommen und Vermögen weltweit in den vergangenen 30 Jahren extrem zugenommen. Mittlerweile besitzen die weltweit 80 reichsten Personen genauso viel wie ärmere Hälfte der Menschheit, also rund 3,6 Milliarden Menschen. 2009 besaßen die 1 % -Reichsten 44 % des weltweiten Reichtums, 2014 bereits 48 %. Und die Schwere zwischen Arm und Reich wird weiter wachsen: Bereits 2016 werden die 1 %-Reichsten mehr besitzen als die restlichen 99 %. Zur Bekämpfung sozialer Ungleichheit fordert Oxfam die Umsetzung seines zehn Hauptpunkte umfassenden Aktionsplans, u.a. die Angleichung von Einkommen und eine faire Besteuerung, die eine Entlastung des Faktors Arbeit und eine höhere Besteuerung von Reichen sowie das Eindämmen von Steuerflucht und -betrug umfasst. Infos/ Daten/ Downloads: Oxfam-Bericht zur sozialen Ungleichheit
|
|
Existenzminimumbericht 07.11.12 (107) |
Bundesregierung: Neunter Existenzminimumbericht für 2014 Nach Vorgaben des Bundesverfassungsgerichts muss das Existenzminimum (Ernährung, Unterkunft, Heizkosten, Bildung und soziale Teilhabe) von der Einkommensteuer freigestellt werden. Deshalb hat die Bundesregierung alle zwei Jahre einen Bericht über das Existenzminimum von Erwachsenen und Kindern vorzulegen. Im 9. Bericht für das Jahr 2014 werden folgende sog. "sächliche" Minima berechnet: Alleinstehende: 8352€ (= "Grundfreibetrag" in $32a EStG); Ehepaare 14016 €; Kinder: 4634 €. Bei Kindern kommt hinzu ein Freibetrag von 2640 € für den Bedarf an Betreuung, Erziehung und Ausbildung, zusammen also ein Kinderfreibetrag von 7008 € pro Kind. Vom Einkommen werden zunächst die Freibeträge für Kinder abgezogen, vom verbleibenden Rest ist dann nur der Teil oberhalb des Grundfreibetrags zu versteuern (ausführliche Erklärungen und Rechnungen in: Einkommensteuer) Download : 9. Existenzminimumbericht für 2012 [BMF 7.11.12]
|
|
Existenzminimumbericht 30.05.11 (106) |
Bundesregierung: Achter Existenzminimumbericht für 2012 Nach Vorgaben des Bundesverfassungsgerichts muss das Existenzminimum (Ernährung, Unterkunft, Heizkosten, Bildung und soziale Teilhabe) von der Einkommensteuer freigestellt werden. Deshalb hat die Bundesregierung alle zwei Jahre einen Bericht über das Existenzminimum von Erwachsenen und Kindern vorzulegen. Im 8. Bericht für das Jahr 2012 werden folgende sog. "sächliche" Minima berechnet: Alleinstehende: 8004 € (= "Grundfreibetrag" in $32a EStG); Ehepaare 16009 €; Kinder: 4368 €. Bei Kindern kommt hinzu ein Freibetrag von 260 € für den Bedarf an Betreuung, Erziehung und Ausbildung, zusammen also ein Kinderfreibetrag von 7008 € pro Kind. Vom Einkommen werden zunächst die Freibeträge für Kinder abgezogen, vom verbleibenden Rest ist dann nur der Teil oberhalb des Grundfreibetrags zu versteuern (ausführlich Erklärungen und Rechnungen in: Einkommensteuer) Download : Achter Existenzminimumbericht für 2012 [dipbt 30.05.11]
|
|
|
|
|
| Jahrgang: | 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
|
|
|
Ungleichheit  Arbeitsblatt März 10 (39) |
MUED:
Umverteilung: Schere zwischen Arm und Reich.
Ungleichheit macht krank Ausgehend von einer Infografik und einem Text in der FR vom 15.09.09 untersucht das MUED-Arbeitsblatt die Frage, ob in Deutschland "die Armen immer ärmer und die Reichen immer reicher" werden. Bei der Lösung werden elementare mathematische Verfahren (Prozentrechnung, lineare Funktion und ihr Anstieg) verwendet. Thema sind auch schlecht erstellte Grafiken, die zu falschen Schlussfolgerungen verleiten, und fehlerhafte Interpretationen von Statistiken. Das Arbeitsblatt eignet sich für den Mathematikunterricht ab Jahrgang 9. MUED-Arbeitsblatt 03/2010: Download (pdf, 98 KB)
|
|
|
|
|
| Jahrgang: | 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025 2026 Alle |
Anmerkungen werden im obigen Text durch
[n] markiert, wobei n eine interne Nummer ist, die der zeitlichen Reihenfolge der Einführung der Anmerkungen [1], [2], [3], ..., folgt, die im Zuge von Ergänzungen abweichen kann von der Reihenfolge im Text. Durch einen Klick auf [n] gelangt man an die Textstelle der Anmerkung. Bei sich möglicherweise verändernden Quellen (Websites) wird das Datum des Zugriffs (Z TT.MM.JJ) notiert, ansonsten das interne Datum [TT.MM.JJ] der jeweiligen Quelle, sofern vorhanden. |
||
| [1] | Staatsfinanzen: öffentliche Haushalte 2008 bis 2012 [xls, Globus 4874 vom 29.03.12] | |
| [2] | Steuerspirale 2011 [xls, Globus 5019 vom 14.06.2012] | |
| [3] | Steuern 2010 und Sozialabgaben 2011 [FR-Infografik 21.09.12, S.3] | |
| [4] | Daten: siehe [2]: Die durch das EStG definierte Einkommensteuer ist dort aufgeteilt (in Mrd. €) Lohnsteuer 139,749, (veranlagte) Einkommensteuer 31,996, nicht veranlagte Steuern vom Ertrag 18,136, Abgeltungssteuer auf Zins-u. Veräußerungserträge, zusammen: 197,901, erhöht um 5,5 % Solidaritätszuschlag ergibt 208,786, das sind 36,4 % von 573,351. Die Quelle in [3] weist für 2010 sogar 38,6 % Einkommensteuer aus, mgw. kommen also noch weitere Steueranteile aus anderen Steuerarten in der "Steuerspirale 2011" hinzu. |
|
| [5] | Daten: siehe [4]: Lohnsteuer/EStG-Summe = 139,749 Mrd./ 197,901 Mrd = 70,6 % | |
| [6] | Die 80-20-Relation (Paretoprinzip), die für viele durch Ungleichheit geprägte Verteilungen annähernd gilt, wird also noch deutlich unterschritten. | |
| [51] | Der Grundfreibetrag wird im Einkommensteuergesetz (EStG) als Teil des Jahressteuergesetzes (JStG) festgelegt. Das JStG 2013 basiert auf dem vom Deutschen Bundestag am 29.3.2012 verabschiedeten Gesetz zum Abbau der "kalten Progression". Dieses Gesetz scheiterte aber im Bundesrat und am 12.12.12. auch im Vermittlungsausschuss, der aber empfahl, den Grundbeibetrag zu erhöhen und den Tarif entsprechend anzupassen, wobei allerdings die Eckwerte (Eingangssteuersatz, Grenzsteuersatzverlauf, Spitzensteuersatz, Reichensteuer) gleichbleiben [s. Drucksache 35-13 mit Tarif im Anhang "Drucksache 17/11842"]. Dieser Empfehlung entsprach der Bundestag am 17.01.13 und der Bundesrat am 1.2.13. Diese Reform wird vermutlich im März 2013 in Kraft treten. Der entsprechend geänderte Tarif für 2013 bzw. 2014 ist im Online-Rechner bereits eingebaut. | |
| [52] | siehe [51] | |
| [53] | Das Ernährermodell "Hausfrauen-Ehe" oder "Zuverdiener-Ehe", das durch den Splittingtarif erheblich subvenioniert wird (s.[54],[55]), ist seit Jahren in der Kritik und gilt als nicht mehr zeitgemäß (s.[56]). | |
| [54] | siehe [3] | |
| [55] | Simone Schmollack: Eine Hausfrauenehe ist so teuer wie ein Eigenheim [dlf 19.1.12] | |
| [56] | Der Splittingtarif ist immer mehr in die Kritik geraten, weil er als Folge der demografischen Entwicklung (jede zweite Ehe ist kinderlos) nicht mehr in erster Linie die Kindererziehung in Familien fördert sondern das Ernährermodell "Hausfrauen-Ehe" oder "Zuverdiener-Ehe", das nicht mehr zeitgemäß ist: Trotz häufig guter Ausbildung werden Frauen verleitet, nicht selbst erwerbstätig zu werden oder wegen Mutterschaft ihre Erwebstätigkeit stark einzuschränken oder ganz aufzugeben, wodurch sie in Abhängigkeit vom Ehemann geraten. Im Fall der Trennung (jede 3.Ehe wird geschieden) und im Alter drohen Armut. Außerdem fehlen dem Arbeitsmarkt dringend benötigte gut ausgebildete Fachkräfte. s.a.: Astrid Rothe-Beinlich: Das Ehegattensplitting ist ungerecht und unzeitgemäß [FR 23.05.13, S.10] |
|
| [57] | Die unterschiedliche Bewertung der Familienmitglieder im Familienfaktor wird z.B. in Frankreich genutzt, um die Geburtenrate hoch zu halten (bei rund 2 %), indem die Familien zum 3. Kind motiviert werden dadurch, dass das 3. Kind doppelt so hoch wie das 1. / 2. bewertet wird: Eine Familie mit 2 Erwachsenen und 3 Kindern bekommt in Frankreich den Faktor 4 (= 2 + 0,5 + 0,5 + 1) | |
| [70] | Bundesverfassungsgericht (BVerfG): Urteil zur Grunderwerbsteuer bei Homo-Paaren vom 08.08.2012 a) Pressemitteilung [BVerfG 8.8.12]; b) Überblick Zusammenfassung [tagesschau 8.8.12] |
|
| [71] | Bundesverfassungsgericht (BVerfG): Urteil zum Adoptionsrecht bei Homo-Paaren vom 19.02.2013 a) Pressemitteilung [BVerfG 19.2.13]; b) Überblick Zusammenfassung [tagesschau 19.2.13] |
|
| [72] | Bundesverfassungsgericht (BVerfG): a) Urteil zum Ehegattensplitting vom 07.05.2013, b) Pressemitteilung vom 06.06.2013 |
|
| [73] | Tagesschau: Lindner will Milliarden-Steuerentlastung durchsetzen [ARD 05.06.24] | |
| Exkurse in die Mathematik der Oberstufe | ||
In der Seite oben nur angeführte Sachverhalte werden im folgenden mathematisch begründet. Dabei werden die mit der Einkommensteuer verbundenen Inhalte und Verfahren der Oberstufen-Mathematik kurz kontextbezogen erklärt. Die teils ausgeführten Beweise können auch als Brücke zwischen Oberstufe und Studium dienen, indem vom Funktionsgrafen her anschauliche Aspekte formalisiert und bewiesen und dabei mathematische Schreibweisen und Beweistechniken verwendet werden. |
||
| [81] | Exkurs Mathematik: Grenzsteuersatz Häufig lautet die eher umgangssprachliche Definition des Grenzsteuersatzes in etwa so: "Der Grenzsteuersatz ist der Steuersatz, mit dem der letzte hinzuverdiente Euro zu versteuern ist". Wörtlich genommen liefert diese Definition jedoch oft falsche Ergebnisse, z.B. 0 %, wie die folgende Analyse zeigt. Zur Abkürzung sei x das zu versteuernde Einkommen, f(x) die Steuer und g(x) der Grenzsteuersatz für das Einkommen x. Wird die obige Definition formalisiert, so ist also g(x) = ( f(x+1) - f(x) ) / 1. Durch die in §32a EStG geforderte Abrundung des zu versteuernden Einkommens zu Anfang und des Steuerbetrags am Ende der Berechnung steigt die Steuerfunktion nicht kontiunierlich sondern in Sprüngen um 1 oder mehr, d.h. für viele x gilt f(x+1) = f(x), also g(x) = 0 oder f(x+1) = f(x) +1, also g(x) = 1=100 %. Das gilt für viele x sogar mit einem Differenzwert Δx > 1, also f(x+Δx) = f(x), z.B. beim Tarif 2012: f(x) = 0 für x = 8004 bis 8011 und f(8012) = 1, also für x=8004 bis 8010: g(x) = 0 statt richitg 14 %; g(8011) = 1/1 = 100 % statt richtig 14 %. Die Methode, den Grenzsteuersatz über einen Differenzenquotient mit sehr kleinem Δx zu berechnen, ist also aufgrund der Rundungsprozesse nicht geeignet. Bei z.B. Δx = 1000 (Vorgabewert im.Online-Rechner) spielen die Rundungen keine Rolle mehr, allerdings ist der Differenzsteuersatz dann etwas größer als der Grenzsteuersatz (siehe [90]) Um möglichst gute Ergebnisse zu erzielen, wird der Grenzsteuersatz durch bereichsweises Ableiten der nicht gerundeten Steuerfunktion bestimmt (siehe [89]). |
|
| [82] | Exkurs Mathematik: Änderungsrate, Differenzenquotient, Differentialquotient Der Grenzsteuersatz ist die Änderungsrate des Steuertarifs. Bezeichnet f die Steuerfunktion, x das zu versteuernde Einkommen und Δx eine kleine Einkommensdifferenz, so gilt nach Definition aus der Differentialrechung: Grenzsteuersatz (x) = f´(x) = Grenzwert von f(x+Δx) / Δx für Δx → 0 Diese Grenzwertbildung funktioniert aber nur, falls die in §32a EStG vorgeschriebene Abrundung auf volle Euro unterlassen wird und die dort bereichsweise angegebenen Teilfunktionen verwendet werden. Der Grenzsteuersatz ist dann der Anstieg der jeweiligen Teilfunktion, also deren 1.Ableitung. Zur Ableitung der bereichsweise definierten Steuerfunktion siehe [89]. Zur Berechnung des Grenzsteuersatzes mittels Differenzenquotient f(x+Δx) / Δx siehe auch [81], [90] . Der Online-Rechner erstellt nach Eingabe von x und Δx eine Steuertabelle, die alle Steuerbeträge und Steuersätze (Effektiv-, Grenz- und Differenzsteuersatz) nach Grund- und Splittingtarif zusammenstellt. |
|
| [83] | Exkurs Mathematik: Stetigkeit einer bereichsweise definierten Funktion Im Folgenden wird vorausgesetzt, dass die Abrundung beim Einkommen und Steuerbetrag unterbleibt. Die Steuerfunktion ist dann eine bereichsweise definierte Funktion, die so konstruiert ist, dass sie überall stetig ist: die Teilfunktionen innerhalb des jeweiligen Bereichs sind stetig (Gerade oder Parabel). Die Parameter sind so bestimmt bzw. berechnet, dass die Teilgrafen an den Rändern der Bereiche nahtlos (ohne Sprung) ineinander übergehen. |
|
| [84] | Exkurs Mathematik: Definition von Parabeln; Horner-Schema; lineare Transformation Die Teilstücke der Steuerfunktion in den Progressionszonen sind Parabeln 2. Ordnung. Sie werden gemäß Horner-Schema f(x) = (ay + b) y + c definiert, was die Berechnung erleichtert. Außerdem wird noch die lineare Transformation y = ( x - g) / 10000 durchgeführt. Da die Steuerfunktion ingesamt stetig sein soll (kein Spung an den Rändern), muss die 1. Parabel bei 0 starten, d.h. c1 = 0. |
|
| [85] | Exkurs Mathematik: Lineare Funktion |
|
| [86] | Exkurs Mathematik: Lineare Appoximation einer konvexen Funktion
Es lässt sich allgemein beweisen, dass eine Funktion konvex ist, falls ihr Anstieg größer wird (linksgekrümmt: wie Parabel in der Progressionszone) oder mindestens gleich bleibt (Gerade: wie in der Proportionalzone). Aus der Konvexität des Grundtarifs kann abgeleitet werden, dass bei Ehepaaren der Splittingtarif kleiner oder gleich der Einzelversteuerung nach Grundtarif ist: |
|
| [87] | Exkurs Mathematik: Ableitung einer verketteten Funktion |
|
| [88] | Exkurs Mathematik: Lineare Funktion: Vergeich von Splitting- und Grundtarif für große x |
|
| [89] | Exkurs Mathematik: Ableitung einer bereichsweise definierten Funktion Der Grenzsteuersatz ist die Änderungsrate des Steuertarifs, also gleich dem Anstieg der Steuerfunktion, der bestimmt wird durch bereichsweises Berechnen der 1. Ableitung (Differentialrechung-Regeln) der Teilfunktionen, die im Folgenden mit f0´(x) bis f4´(x) bezeichnet werden: (0) Nullzone: f0´(x) = 0 (1) Progressionszone 1: f1´( x) = (2 a1 • y + b1) / 10000; y = (x − g0) / 10000 (2) Progressionszone 2: f2´( x) = (2 a2 • z + b2) / 10000; z = (x − g1) / 10000 (3) Proportionalzone 1: f3´(x) = m1 (4) Proportionalzone 2: f4´(x) = m2. Die in § 32a EStG vorgesehene Berechnung der Zwischenwerte y, z kann natürlich unterbleiben, in dem der jeweilige Zwischenwert im Funktionsterm ersetzt wird durch seinen Term: (0) Nullzone: f0´(x) = 0 (1) Progressionszone 1: f1´( x) = ( 2 a1 • (x − g0) / 10000 + b1) / 10000 (2) Progressionszone 2: f2´( x) = ( 2 a2 • (x − g1) / 10000 + b2) / 10000 (3) Proportionalzone 1: f3´(x) = m1 (4) Proportionalzone 2: f4´(x) = m2. Die Grenzsteuerfunktion ist in g0 und g3 nicht stetig (anschaulich: sie macht dort einen Sprung), denn f0´(g0) = 0 und f1´(g0) = b1/10000 > 0, f3´(g3) = m1 und f4´(g3) = m2 > m1 d.h. die Steuerfunktion f verläuft in g0 und g3 nicht glatt sondern eckig. In g1 und g2 ist die Grenzsteuerfunktion f ' stetig, d.h. die Steuerfunktion f verläuft dort glatt, weil die Parameter so festgelegt bzw. berechnet wurden. |
|
| [90] | Exkurs Mathematik: Differenzsteuer und Grenzsteuer Bezeichne x das abgerundete zu versteuernde Einkommen, E(x) die Einkommensteuer zu x (berechnet mittels Grund- oder Splittingtarif). Der effektive Steuersatz, mit dem eine Einkommenserhöhung Δx versteuert wird, ist dann der Differenzenquotient ΔE / Δx, genauer D(x,Δx) = ( E(x+Δx) - E(x) ) / Δx Ist Δx nicht zu groß und auch nicht zu klein (siehe [82]) ist D(x,Δx) nur etwas etwas größer als der Grenzsteuersatz G(x). Zum Vergleich wird im Online-Rechner mit Δx = 1000 € als Vorgabewert gerechnet. Bei festem Δx = 1000 € ist der Abstand von D(x,Δx) und G(x) für x = Grundbetrag + 1 am größten, z.B. Grundtarif 2010-12 : D(8005) = 14,90 %; G(8005) = 14,00 %. Mit wachsendem Δx weicht D(x,Δx) immer mehr von G(x) ab, bei großem Δx sollte der Differenzenquotient ( E(x+Δx) - E(x) ) / Δx tatsächlich berechnet und nicht über G(x) geschätzt werden. Um diese Rechung einfach durchführen zu können, kann neben x auch Δx im Online-Rechner eingegeben werden. Wird die Abrundung beim Steuertarif unterlassen gilt: G(x) = Grenzwert von D(x) für Δx → 0, s. [82] |
|
| [91] | Exkurs Mathematik: Kalte Progression Bezeichne x das zu versteuernde Einkommen und Δx den Einkommenszuwachs. Dieser wird mit dem Differenzsteuersatz D(x,Δx) besteuert (s.[90]), nach Steuern verbleibt also ein Zuwachs von Δx • (100 % - D(x,Δx)). Dieser ist positiv, da D(x,Δx) < 100 %: D(x,Δx) ist nur etwas größer als der Grenzsteuersatz G(x) (s.[90]), dessen Maximum der Spitzensteuersatz ist und der liegt aktuell bei 45 %. Die Progression im Steuertarif kann also selbst im Extremfall nur bewirken, dass der Lohnzuwachs um ca. 45 % reduziert wird. |
|
| [92] | Kalte Progression: Rechenbeispiel mittels Grundtarif für das Jahr 2014 in Euro: Bezeichnungen wie unter [91] Das zu versteuernde Einkommen (zvE) sei am Anfang x = 40.000. Nach Abzug v. 8949 Steuer verbleiben 31060 Kaufkraft. Nach einer Lohnerhöhung von z.B. p = 4 % ist der Lohnzuwachs Δx = x • p = 1600, also . das erhöhte zvE x • (1 + p) = 41600 Euro, abzügl. 9524 Steuern verbleiben nach Steuern 32076. Laut Steuertabelle ist der Diffenzsteuersatz d = D(40.000, 1.600) = 0,365, also 1 - d = 0,635 Bezeichnet i die Inflationsrate, die den Zuwachs nach Steuern auf 0 bringt (Break-Even-Rate), so folgt: x • p • (1 - d) = x • (1 + p) • i, also i = (1 - d) • p / (1 + p) = 0,635 • 0,04 / 1,04 = 2,44 % Kontrolle: 2,44 % von 41.600 = 1015; 32076 - 1015 = 31061 2,45 % von 41.600 = 1019; 32076 - 1019 = 31057 Aus der Lohnerhöhung p und dem Differenzsteuersatz d kann also auf einfache Weise die Break-Even-Rate der Inflation i berechnet werden. Eine Inflation höher als die Break-Even-Rate führt zu Kraufkraftverlust trotz Lohnerhöhung. Bei einer normalen Lohnerhöhung bleibt der Lohnzuwachs Δx so klein, dass der Differensteuersatz d nur wenig über den Grenzsteuersatz g liegt. Wird also in der Formel d durch g ersetzt, steigt i ein wenig, z.B. mit den obigen Werten : i = 0,639 • 0,04 / 1,04 = 2,46 %. Da g mit steigenden Einkommen wächst bis zum Spitzensteuersatz von 45 %, sinkt die Break-Even-Rate auf minimal 0,55 • 0,04 / 1,04 = 2,12 %, etwas mehr als die Hälfte der Lohnerhöhung. Falls nur überschlägig gerechnet wird, kann (1+p) durch 1 ersetzt werden, wodurch sich das Ergebnis etwas erhöht: i = (1 - g) • p = 0,639 • 0,04 = 2,56 %. Zum überschlägigen Kopfrechnen kann dann noch der 1- g zur Kompensation nach unten abgerundet werden: 0,63 • 0,4 = 2,52. |
|
|
|
||
| Stand: 21.12.23/zgh |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
||||||||||||||||||||||
| Kontakt | über uns | Impressum | Haftungsausschluss | Copyright © 1999 - 2026 Agenda 21 Treffpunkt | |||